
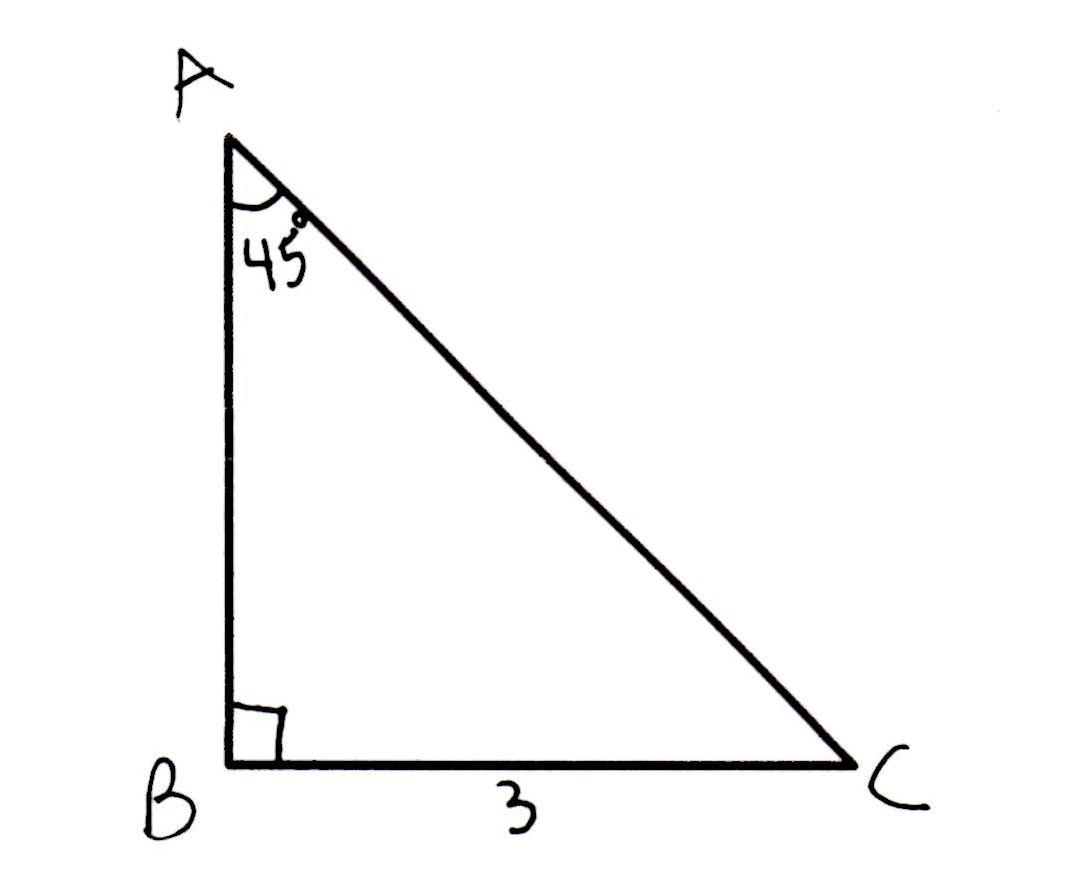
∠BAC and ∠ABC is known as interior opposite angles of ∠ACD Here, ∠ACD and ∠ACB are adjacent supplementary angles. Here, ∠ACD is known as exterior angle and ∠ACB is known as interior angle. In the above figure ABC is a triangle and its side BC is extended to D. Similarly, transversal AC intersect them at point E and C. Here, DE || BC and transversal AB intersect them at point B and D. In triangle ABC, we have ∠A = 30°, and ∠C = 40° In below given figure DE || BC, ∠A = 30°, and ∠C = 40°. Let's assume the other acute angle is p°.Īs we know, sum of all the angles of a triangle is 180°.Įxample 6. One of the acute angles of a right-angled triangle is 50°. Let's assume PQR is the triangle and ∠P, ∠Q, and ∠R it's angles.Īs it is a right-angled isosceles triangle, it's ∠P = ∠QĮxample 5. Determine the measures of all the angles. The sum of two angles of an isosceles triangle is equal to it's third angle. So, the angles of the triangles are 40°, 60° and 80°.Įxample 4. Let's assume all the three angles are 2x°, 3x°, and 4x°.Īs we know sum of all the angles are equal to 180° If the angles of a triangle are in the ratio 2 : 3 : 4, then find the three angles of the triangle. Find all the angles of right-angled isosceles triangle. Let's assume the third angle is 'x'.Įxample 2. Two angles are provided, they are 65° and 45°.

As we know sum of all the angles of a triangle is 180°. If two angles of a triangle are 65° and 45°, then find the third angle. Let's see some examples to understand these properties.Įxample 1.

A triangle can not have more than one right angle.The sum of the angles of a triangle is 180°.Let's assume a, b and c are the three sides of a triangle, then its perimeter = a + b + c The sum of the lengths of the sides of a triangle is called its perimeter. Here, triangle PQR is an obtuse angled triangle, where ∠PQR is an obtuse angle. Triangle ABC is a right-angled triangle, where ∠ABC = 90°Ī triangle whose one angle is more than 90° is known as obtuse-angled triangle. Here, AB = BC = AC and ∠ABC = ∠BAC = ∠ACB = 60°Ī triangle whose all the angles are acute is known as acute angled triangle or acute triangle.Įquilateral triangle is also an acute angled triangle.Ī triangle whose one angle is a right angle is known as a right-angled triangle. Figure below shows an example of equilateral triangle. Figure below shows an example of isosceles triangle.Ī triangle whose all sides are equal to one another is known as equilateral triangle. Figure below shows an example of scalene triangle.Ī triangle whose two sides are equal is known as an isosceles triangle. Different types of triangles are given below.Ī triangle whose all three sides length are not equal is known as scalene triangle. Triangles are named on the basis of the lengths of their sides and the measures of their angles. Sum of Lengths of Two Sides of a Triangle


 0 kommentar(er)
0 kommentar(er)
